
Essence of linear algebra (2016)
Back to main
1. Vectors, what even are they?
Kicking off the linear algebra lessons, let's make sure we're all on the same page about how specifically to think about vectors in this context.
0
0min
August 6, 2016

2. Linear combinations, span, and basis vectors
The fundamental vector concepts of span, linear combinations, linear dependence, and bases all center on one surprisingly important operation: Scaling several vectors and adding them together.
0
0min
August 7, 2016

3. Linear transformations and matrices
Matrices can be thought of as transforming space, and understanding how this work is crucial for understanding many other ideas that follow in linear algebra.
0
0min
August 7, 2016

4. Matrix multiplication as composition
Multiplying two matrices represents applying one transformation after another. Many facts about matrix multiplication become much clearer once you digest this fact.
0
0min
August 9, 2016

5. Three-dimensional linear transformations
What do 3d linear transformations look like? Having talked about the relationship between matrices and transformations in the last two videos, this one extends those same concepts to three dimensions.
0
0min
August 10, 2016

6. The determinant
The determinant of a linear transformation measures how much areas/volumes change during the transformation.
0
0min
August 11, 2016

7. Inverse matrices, column space and null space
How to think about linear systems of equations geometrically. The focus here is on gaining an intuition for the concepts of inverse matrices, column space, rank and null space, but the computation of those constructs is not discussed.
0
0min
August 16, 2016

8. Nonsquare matrices as transformations between dimensions
Because people asked, this is a video briefly showing the geometric interpretation of non-square matrices as linear transformations that go between dimensions.
0
0min
August 16, 2016

9. Dot products and duality
Dot products are a nice geometric tool for understanding projection. But now that we know about linear transformations, we can get a deeper feel for what's going on with the dot product, and the connection between its numerical computation and its geometric interpretation.
0
0min
August 24, 2016

10. Cross products
This covers the main geometric intuition behind the 2d and 3d cross products.
0
0min
September 1, 2016

11. Cross products in the light of linear transformations
For anyone who wants to understand the cross product more deeply, this video shows how it relates to a certain linear transformation via duality. This perspective gives a very elegant explanation of why the traditional computation of a dot product corresponds to its geometric interpretation.
0
0min
September 3, 2016

12. Cramer's rule, explained geometrically
This rule seems random to many students, but it has a beautiful reason for being true.
0
0min
March 17, 2019

13. Change of basis
How do you translate back and forth between coordinate systems that use different basis vectors?
0
0min
September 11, 2016

14. Eigenvectors and eigenvalues
A visual understanding of eigenvectors, eigenvalues, and the usefulness of an eigenbasis.
0
0min
September 15, 2016
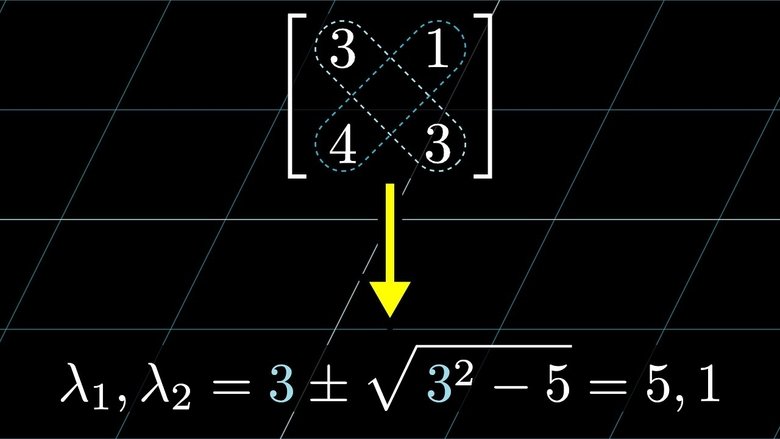
15. A quick trick for computing eigenvalues
How to write the eigenvalues of a 2x2 matrix just by looking at it.
0
13min
May 7, 2021

16. Abstract vector spaces
This is really the reason linear algebra is so powerful.
0
17min
September 24, 2016